Pérdidas de calidad en cajas acústicas

Existen 3 tipo de pérdidas que pueden afectar el tamaño final de tu caja, estas son, pérdidas por fuga ( $Q_L$ ), pérdidas por absorción, relacionadas con el amortiguamiento del material ( $Q_A$ ) y pérdidas de ventilación que pueden ser producidas por el ducto ( $Q_P$ ). Estas pérdidas forman parte de la pérdida total del sistema ( $Q_B$ ) la cual se calcula de la siguiente forma para cualquier caja porteada.

\tag{1} \frac {1}{Q_B}=\frac {1}{Q_L}+\frac {1}{Q_A}+\frac {1}{Q_P}

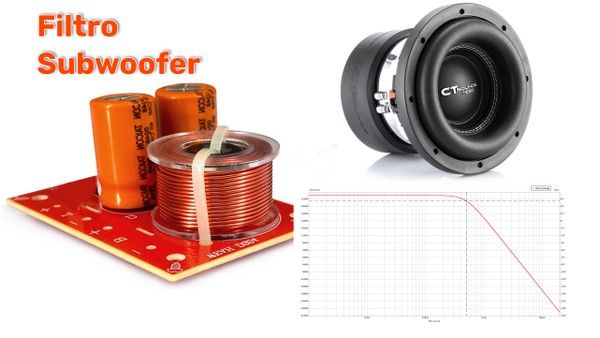
En la práctica los valores de $Q_A$ y $Q_P$ son pequeños y no aportar un valor significante de pérdidas, esto es asumiendo que se ha usado un material suficientemente rígido que no permite la amortiguación. Ya que las pérdidas solo dependen de las pérdidas por fuga, el efecto de estas pérdidas tienen un efecto en la respuesta en frecuencia del parlante seleccionado mostrado en la Figura 1.

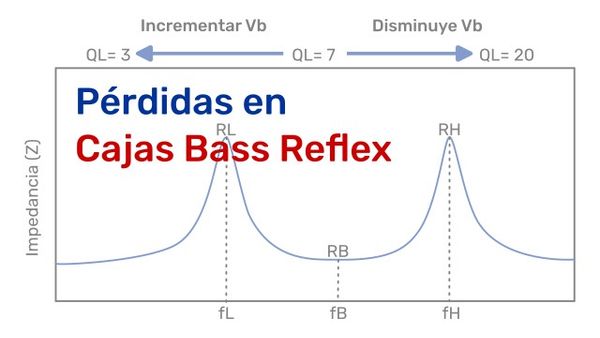
Las pérdidas por fuga nunca se pueden evitar, sin embargo, para corregir esto asuma un valor típico de $Q_L = 7$ y construya la caja en base a esto, luego mida la respuesta en frecuencia, si las medidas están cerca a $Q_L = 7$ no se hace ningún cambio adicional, pero si el valor es mayor o menos se debe recalcular el tamaño de la caja con un nuevo valor de $Q_L$ . El diagrama de la Figura 2, muestra la relación entre el tamaño de la caja y el valor de $Q_L$ .

Una buena práctica de sintonización es usar una caja más grande de lo esperado y disminuir volumen poco a poco hasta encontrar el valor de sintonía correcto.

¿Como sabemos que la caja está bien sintonizada?

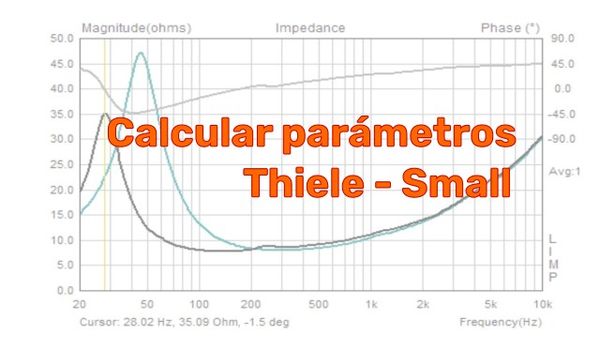
Para saber esto, es necesario medir la impedancia de la caja, para esto es necesario desconectar el crossover y medir la respuesta de la impedancia con un barrido de frecuencia desde 20 Hz a 20KHz, con esto se puede obtener la gráfica de la Figura 3.

Una vez obtenido los valores de la gráfica de la Figura 3 se pueden aplicar las siguientes ecuaciones.

\tag{2} f_{SB}= \frac{f_L f_H}{f_B}

\tag{3} h= \frac{f_B}{f_{SB}}

\tag{4} \alpha= \left [ \left ( \vcenter{ \frac{f_B}{f_L} } \right )^2 -1 \right] \left [ 1- \left ( \vcenter{ \frac{f_B}{f_H} } \right )^2 \right]

Finalmente para calcular el valor de $Q_L$ usamos la ecuación 7, Conociendo los valores de $Q_{ES}$ y $Q_{MS}$ que son calculados con la curva de impedancia del parlante o usando los datos del fabricante. Estos valores deben ajustarse a la masa de aire a la que están expuestos en la caja.