Maykol Rey

Ing. Electrónico

05/07/2024

Control de impedancias en líneas de transmisión

La impedancia es la oposición al flujo de corriente, está formado por elementos capacitivos, inductivos y resistivos. se puede expresar matemáticamente con la siguiente expresión.

Z = R + jX

Donde X es un factor imaginario compuesto por cargas reactivas o inductivas o también la sumatoria de ambos. por ejemplo en un circuito se puede tener lo siguiente:

En este caso la impedancia es:

Z=R+(j2 \pi fL)+\frac {1} {(j2 \pi fC)}

Como pueden ver, esto solo tiene efecto en presencia de frecuencia, si calculamos la impedancia de este circuito ante una señal DC, la impedancia será infinita debido a la presencia del capacitor.

Una vez comprendido este concepto de impedancia, veamos un componente común, una resistencia. Podríamos decir que su impedancia es igual al valor de su resistencia, sin embargo, esto es aceptable sólo cuando la frecuencia tiende a cero, debido que al aumentar la frecuencia aparecen componentes reactivos.

Como pueden ver, una resistencia común se convierte en un circuito más complejo a medida que aumenta la frecuencia.

Impedancia característica

Una pista de una PCB puede considerarse una línea de transmisión el cual se puede expresar como una sumatoria a infinito del siguiente circuito.

Esto se cumple a lo largo de toda la pista siempre que sus características físicas sean las mismas durante todo el recorrido, con esto podemos.

Se debe considerar que la impedancia es independiente de la frecuencia y de la longitud en condiciones digitales.

Z= \sqrt{\frac {R+jwL}{G+jwC}}

quedando entonces

Z= \sqrt{\frac {L}{C}}

El concepto que ya todos conocemos es que para alcanzar la máxima transferencia de potencia, la impedancia de la fuente debe ser igual a la impedancia de la carga.

Z_{out}=Z_{in}

Debido a que en sistemas digitales se desprecia la resistencia la expresión quedaría de la siguiente manera.

R_{out}=R_{in}

La mayoría de los dispositivos electrónicos tienen una impedancia de 50 Ohm, es por esta razón que el diseñador de PCB debe considerar las características físicas de las pistas, tales como; ancho de la pista,distancia al plano de tierra, coeficiente dieléctrico, espesor del cobre, entre otros.

Es importante recordar que a altas frecuencias las señales viajan por el dieléctrico y el cobre solo se usa como una guía de onda.

Cuándo debe considerarse una línea de transmisión

Lo que define el uso de una línea de transmisión está relacionado con la velocidad de conmutación de una señal digital, pueden consultar la IPC-2141A para tener más detalles sobre esto.

En las señales digitales los flancos de subida o bajada tienen componentes frecuenciales mucho más rápidos que la frecuencia de trabajo, es por esta razón que se usa el tiempo de subida para calcular la frecuencia máxima de trabajo.

De esta forma podemos tener la siguiente expresión

F_{max(GHz)}=\frac {0.35} {tr(ns)}

En caso de no conocer el valor de Tr, se puede aproximar usando el 7% del periodo de la señal, quedando la siguiente forma.

F_{max(GHz)} = 5*F_{clock}

con este dato podemos calcular la longitud límite, la cual queda de esta forma:

L_{min}(mm) = \frac {V_{propagación}} {7F_{max(GHz)}} = = \frac {122,449 * Tr_{(ns)}} {\sqrt{ \varepsilon_r }}

o también

L_{min}(mm) = \frac {8,571} {\sqrt{ \varepsilon_r }F_{max(GHz)} }

Todo esto significa que toda pista que supere esta distancia debe pasar por un proceso de adaptación de impedancia.

Veamos un ejemplo:

El USB 2.0 tiene una velocidad de transmisión de 400 Mbps y se transmiten 2 bits por cada ciclo, con lo que tenemos una frecuencia de 200 MHz. Si usamos FR4 con una constante dieléctrica de 4, se obtiene una longitud límite de 21 mm, esto significa que toda pista que supere los 21 mm deben ser adaptadas.

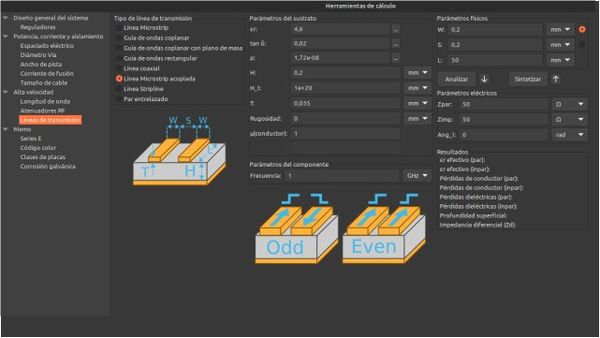
Tipos de líneas de transmisión

Existen 2 grupos de líneas de transmisión, la microstrip y las stripline, el resto son derivaciones de estas.

Microstrip

Stripline

Si la altura del dieléctrico es más pequeña aumenta la contención de las ondas electromagnéticas, lo que evita que interfiera con otras señales. Usando los parámetros físicos y geométricos de la pista se pueden obtener las siguientes expresiones.

Z= \frac {87}{\sqrt{\varepsilon_r + 1.41}}* \ln {\frac {5.98*h}{0.8*W+t}}

T_{pd} = 3.333 * \sqrt{0.475* \varepsilon_r + 0.67}

$h$ =altura del dieléctrico
$w$ = ancho de la pista
$t$ = espesor de la pista
$T_{pd}$ = retardo de la propagación

Es importante que a pesar de tener estos cálculos, es necesario pedir una validación al fabricante, debido a que es posible que existan algunos cambios en el proceso de fabricación.

Parámetros que influyen en la adaptación de impedancia

Espesor del dieléctrico
Ancho de la pista
Espesor de la pista
Coeficiente dieléctrico

De la siguiente fórmula se deduce que mientras más grande es C menor será la impedancia y viceversa.

Z= \sqrt{\frac {L}{C}}

Como modificar L y C

La fórmula indica que mientras más pequeña sea la altura (h) mayor será la capacitancia.

Si se varía h se puede ver que para valores mas grandes, mas alta la impedancia debido a que la capacitancia se hace más pequeña.

Por otro lado, mientras más pequeño es el ancho (w) del conductor mayor será la inductancia.

En este caso, si variamos el ancho, se puede ver que para valores más pequeños hay más impedancia, debido a la alta inductancia.

Además si el Coeficiente dieléctrico es mayor, mayor será la capacitancia.

Esto es una recopilación de los modelos spice, basado en la sintaxis de creación

Maykol Rey

29/08/2024